Estudios e Investigaciones
Impact of intensive programming training on the development of Computational Thinking in prospective teachers
Impacto de una formación intensiva en programación en el desarrollo del Pensamiento Computacional en futuros/as maestros/as
Impact of intensive programming training on the development of Computational Thinking in prospective teachers
RIED-Revista Iberoamericana de Educación a Distancia, vol. 27, núm. 1, 2024
Asociación Iberoamericana de Educación Superior a Distancia

Esta obra está bajo una Licencia Creative Commons Atribución-NoComercial 4.0 Internacional.
How to cite: González-Martínez, J., Peracaula-Bosch, M., & Meyerhofer-Parra, R. (2024). Impact of intensive programming training on the development of Computational Thinking in prospective teachers.
[Impacto de una formación intensiva en programación en el desarrollo del Pensamiento Computacional en futuros/as maestros/as]. RIED-Revista Iberoamericana de Educación a Distancia, 27(1), 187-208. https://doi.org/10.5944/ried.27.1.37672
Abstract: Training pre-service teachers in their own Computational Thinking (CT) is essential to build with them the discourse of CT didactics and its inclusion in the classroom with children in early childhood and primary education. This research proposes possible solutions to this challenge and analyses the results of an intervention carried out with 71 students from two different cohorts of 2nd year teacher training students. This intervention is based on the intensive practice of coding using visual blocks through a Scratch project during the first part of a semester course. After analyzing the previous and subsequent levels of CT (pre-experimental strategy) by means of a standardized test for its measurement (CTt), it is confirmed that the intensive training experience allows all future teachers to reach a sufficient level of CT, regardless of their previous experience in programming and their initial level of CT (they all end up learning, either by increasing their level of CT or by improving their efficiency). On the other hand, measuring the learning outcomes in the Scratch project, we see a clear relationship between a high resulting CTt level (POST) and a good performance in the block programming learning task, which is evidence that the Scratch project helps to develop the future teachers' CT.
Keywords: computational thinking, programming language, teacher training, evaluation.
Resumen: Formar a los profesores en formación en su propio pensamiento computacional (PC) es fundamental para construir con ellos el discurso de la didáctica del PC y su inclusión en el aula con niños de educación infantil y primaria. Esta investigación plantea posibles soluciones a ese reto y analiza los resultados de una intervención llevada a cabo con 71 alumnos de dos cohortes diferentes de 2.º curso de los grados de magisterio. Dicha intervención se fundamenta en la práctica intensiva de programación por bloques visuales en un proyecto de Scratch durante una primera parte de una asignatura semestral. Analizados los niveles previo y posterior de PC (estrategia pre-experimental) por medio de una prueba estandarizada para su medición (Test PC), se confirma que la experiencia formativa intensiva permite a todos/as los/as futuros/as maestros/as alcanzar un nivel suficiente de PC, independientemente de su experiencia previa en programación y de su nivel inicial de PC (todos acaban aprendiendo, sea aumentando su nivel de PC, sea mejorando su eficiencia). Por otro lado, medidos los resultados de aprendizaje en el proyecto de Scratch, vemos una relación clara entre un nivel alto de PC resultante (POST) y un buen desempeño en la tarea de aprendizaje de programación por bloques, lo que evidencia que el proyecto de Scratch ayuda a desarrollar el PC de los/as futuros/as maestros/as.
Palabras clave: pensamiento computacional, lenguaje de programación, formación de profesores, evaluación.
INTRODUCTION
There is no doubt about the popularity that the concept of Computational Thinking (CT) has acquired in the field of education in recent years. In light of this, it is necessary to conduct a thorough analysis of the concept of CT itself and its educational practice from a research perspective.
When talking about CT, we should certainly pay attention to the work of Seymour Papert (1980), who, at the end of his classic Mindstorms, mentions computational thinking, and refers to learning environments in which the computer is "an object to think with" (p. 182). Traditionally, however, the concept itself is considered to be born with Wing's (2006) seminal definition, a quarter of a century later. Although this is only a conceptual approximation, there is no doubt that it has largely functioned as a definition that points to important elements of CT: "Computational thinking involves solving problems, designing systems, and understanding human behavior, by drawing on the concepts fundamental to computer science." (Wing, 2006, p. 33). However, it is in Wing (2014) where we find a complete definition: "Computational thinking is the thought processes involved in formulating a problem and expressing its solution(s) in such a way that a computer -human or machine- can effectively carry out". This is a definition with very important key ideas: a mental process, the formulation of a problem, the expression of its solution(s), the need for a computer (human or machine); to which are added interesting reflections on abstraction or the importance of CT beyond the concrete contexts of computer science.
On this basis, many authors consider CT to be a core competence for the 21st century (Angeli et al., 2016; European Commission/EACEA/Eurydice, 2012; Fluck et al., 2016). It enables us to develop an effective problem-solving and problem-posing procedure (Fluck et al., 2016) in any dimension of the world we live in, and consequently helps us to understand and live in it (Furber, 2012). In that sense, Grover and Pea (2013) emphasize that computing is a human activity; abstraction helps to focus on the essential and neglect the superfluous; and, consequently, CT promotes the creation of knowledge, creativity and innovation, in all senses and at all levels. Attitudinal elements such as confidence, perseverance or collaboration are also pointed out (Bocconi et al, 2016b). For these reasons, many education systems have decided to include it in the curriculum: Canada, the United Kingdom, Finland, and Australia are examples (Acevedo Borrega, 2016; Bocconi et al., 2016a).
However, what interests us now is to focus on the teachers who must accompany this learning process. In this sense, it is generally accepted that teachers need to be trained specifically in CT; and, because of this common assumption, for more than a decade now, the focus has been on both teacher training itself and the pedagogical models associated with CT (Morreale et al., 2012).
According to Butler and Leahy (2021), the lack of research on the CT training processes of future teachers justifies that this should become a focal point as a matter of priority in order to improve the training of trainers and, consequently, the training of children. To this end, a first part dedicated to CT development is essential before addressing didactic issues; and, based on what we already know, few efforts in this direction yield many results: both in the improvement of CT and in the improvement of attitudes towards it (Bustillo & Garaizar, 2015; González-Martínez et al., 2018; Peracaula-Bosch et al., 2020). There is evidence of a lack of a conceptual basis on CT in teachers (Acevedo-Borrega et al., 2022; Morze et al., 2022), as well as the need to focus, both in initial and in-service training, on specific technical and conceptual skills (Rich, Mason & O'Leary, 2021) to improve teachers' own performance in formal educational contexts ( Collado-Sánchez et al., 2021). Research, in fact, tells us that the improvement in specific training not only improves self-perception, but that this generates a perfect spiral: the improvement of their own CT allows teachers to feel more confident, both in their CT practice and in their teaching practice; and this confidence effectively improves their actual competence (Rich, Larsen & Mason, 2021), even in short training experiences (Pala & Türker, 2021), which must focus, to be effective, on elements such as age or the correct design of the activities (Li, 2021). This is supported by the TPACK model (Mishra & Koehler, 2006), which is based on the need for trainers to have a combination of three types of knowledge: content, pedagogical, and technological. In this case, the adequate level and development of CT would correspond to content knowledge and a lack of it would represent a barrier in the teaching process deployed by the teacher. In the literature review conducted by Mason and Rich (2019), 21 studies are analyzed (12 on pre-service teachers and 9 on in-service teachers, with a total of 802 participants) in which the results indicate that factors such as teachers' perceived CT self-efficacy increase with training that promotes its development, and this has an impact on their understanding of the concept and their ability to design and evaluate CT learning experiences. These results are further corroborated in Rich, Mason and O'Leary (2021) in a study of 127 teachers, which is consistent with Lamprou and Repenning's (2018) study of 471 pre-service teachers. In this study, CT training, focusing, for example, on the concepts of abstraction, analysis, and automation, drastically increases teachers' confidence in their ability to teach CT. Thus, the perception of self-efficacy in CT also leads to self-efficacy in the ability to teach CT. Finally, it is noteworthy to pay attention to a recent study with 245 teachers from 47 schools in Hong Kong (Kong et al., 2023) who were trained in CT development during one school year and were followed up in their classroom implementation, offering a direct analysis of the relationship between teachers' training, teaching performance and student learning. The study corroborates the need for teacher training in CT and its development, validating training programmes based on block and mixed programming environments and recommending continuous support during teaching through platforms, mentoring and repositories of materials. In this regard, we take up a vision that seems to us to be very appropriate, proposed by Estebanell et al. (2018), in which they point out that, before facing the issue of CT didactics, trainee teachers must consolidate themselves as CT users and as reflective users (i.e. develop their own CT in a reflective way) before going on to develop their dimension as CT teachers or reflective CT teachers, which would be the last stage. We also know that providing clear models that provoke reflection can be helpful as a strategy to compensate for the lack of specific training (Dobgenski & Garcia Silva, 2022). However, the solution is not simple, and there are many issues that still need to be clarified. On the one hand, as in any disciplinary didactics subject, it is important not to stop at the development of disciplinary knowledge, but to jump to didactic issues; therefore, the time devoted to disciplinary knowledge must be very limited and targeted. On the other hand, precisely for this reason, it seems sensible to think that, in terms of efficiency, the effort we devote to the development of CT should allow us to learn the use of tools that we can then also use in the didactic approach and for the conceptualization of reflective processes (Pérez-Marín et al., 2020).
Nevertheless, dedicating an intensive first part of a course or subject to CT development in teacher training is not easy, nor can its results be taken for granted (the conceptualization of CT is complex, and its development is not immediate). It is in this context that this research proposal was born; in it, we set out, as a general objective, to analyze the development of CT through an intensive block programming activity in the university training of student teachers, prior to training in the didactics of CT (which is, in fact, the final objective in teacher training).
So, at the end of this reflection, we come to our research question: is it possible to develop the CT of future teachers through training in Scratch, at the beginning of a course, before moving on to didactic aspects?
To this general question, we can add the following questions, which will help us to go deeper into our object of study:
- How do the different starting points of learners in CT development influence the results?
- Is it possible to relate the CT results to some of the competences and skills required for the development of a programming project with Scratch?
- The CT test we will use measures understanding of languages and computational logic from less to more complex configuration challenges. From this, does having created a complex program, with ingenious and optimized solutions that works, relate to the CT results?
METHODS AND INSTRUMENTS
To conduct this research, we decided to work with two study groups composed of second-year students of the degrees of Early Childhood Education (ECE) and Primary Education (PE) at the University of Girona (some of them from the double degree of ECE and PE). The study was carried out within the framework of the course Computational Thinking and Programming of the Information and Communication Technologies degree minor taught during the second semester of the 2020/21 and 2021/22 academic years. The total number of participants was 71, of whom 36 took the subject in the first cohort and 35 in the second.
As for their prior knowledge of programming and robotics, the students have received an introduction to CT related activities with some practical exercises (demonstrations of educational robotics and an introduction to programming with Scratch) during the first year of their studies as part of a compulsory course. In addition, the test asks students whether they have previous experience in programming activities, referring to any possible training they may have received in the stages prior to entering university, both in formal academic contexts and outside it.
In relation to the research design and its fit with the learning experience (aimed at developing CT), a pre-experimental design was proposed in terms of the application of one of the instruments (the CT Test, which we will detail below) and an ex post facto collection of information in terms of the analysis of part of the evaluation activities handed in by the participants at the end of the experience (programming project with the Scratch visual block language, https://scratch.mit.edu/). As for the pre-experimental strategy, the CT Test was applied at the beginning of the course and at the end of the first part (February to April), dedicated to the implementation of different activities to develop the students' CT, before tackling the second part of the semester, dedicated to the development of didactic competences to teach CT to kindergarten and primary school children. In a summarized version, this training and research strategy considered the following sequence:
-
Weeks 1 to 4: CT Introduction activities
- Unplugged CT activity
- CT Test (PRE)
- Theoretical analysis and reflection
- Block programming workshop (TurtleStitch, https://www.turtlestitch.org/) in 2021 and MicroBlocks (https://microblocks.fun/) in 2022
- Weeks 5 to 9: Tutorials and Scratch exercises starting from a basic level (programming the movement of an element or character) and gradually increasing in complexity: interaction with and between characters, sensors, variable conditionals, operators, functions and modularization, and use of the graphic editor for the creation and modification of characters and scenarios.
- Weeks 5 to 10: Development in individual and autonomous work of a Scratch project that simulates a scientific phenomenon of free choice (examples include: water cycle, phases of the moon, development of a plant, fall of a meteorite in the presence of unsuspecting dinosaurs, etc.). The aim is not only to learn how to program but also to emphasize that the fact of having to narrate visually in a precise language is conducive to a deep understanding of the phenomenon to be explained. In terms of programming, students are told that the use of various programmed elements (characters), scenario transitions, and elements characteristic of computer languages, such as conditionals, iteration in loops, operators, variables, and some interactivity with the user, will be valued. During the development of the project, students receive the tutorials indicated in the previous point, tutoring with trainers, and can consult and participate in a forum of doubts, answers, and discoveries for communication and for the exchange of the whole group and the teaching staff.
- Week 11: CT Test (POST)
- Weeks 11 to 14: Design phase: The course continues for a few weeks focusing on the didactics of CT (design and implementation of activities that allow its development), the analysis of which is beyond the scope of this reflection.
As for the instruments, as we said, first, we decided to use an existing instrument, the Computational Thinking Test (CTt, hereafter) validated by Román-González (2016) and Román-González et al. (2018). For this study we have used the adaptation of the original test CTt-RA+B, specifically designed for participants over 14 years of age (Moreno-Leon et al., 2022). The CTt measures, according to its creators, CT understood as follows: "CT involves the ability to formulate and solve problems by relying on the fundamental concepts of computing, and using logic-syntax of programming languages: basic sequences, loops, iteration, conditionals, functions and variables" (Román-González et al., 2017, p. 681). Consequently, it measures the understanding of computational languages and computational logic in configurations from less to more complex. During its resolution, students do not develop their own algorithms or programs, but rather decipher proposed algorithms, generally by answering which of several options solves the challenge of the question. The algorithms are presented in different languages and symbology.
Secondly, the tasks given for the assessment of learning at the end of the first part of this subject were analyzed. A large part of the students' training is devoted to learning visual programming by blocks through different activities and tutorials, among which, due to the complexity and time spent, the creation of a Scratch project that simulates a natural or scientific phenomenon plays a major role.
In order to analyze these tasks, and in relation to the specific research questions of this topic, from the Scratch project that each student developed during the training and the report she or he made on it we extracted the factors that can be related to their CT level according to the parameters measured by the CTt mentioned above, so that we classified them in the categories shown in Table 1. In each of these categories a maximum score of 4 points could be obtained considering the assessment items; therefore, a maximum total score of 12 points could be obtained.
| Categories | Elements of evaluation | Maximum score |
| How the program works and at what level the student understands it | Correct functioning of the program | 4 |
| Use of initial conditions | ||
| Annotated parts of the algorithm reflecting the understanding of actions | ||
| Description of the problems encountered and understanding of the solutions found | ||
| Complexity | Various programmed characters/scenarios | 4 |
| Changes in appearance | ||
| Transitions | ||
| Interactivity | ||
| Optimization and ingenuity | Variety of computer language elements that help and simplify programming: loops, conditionals, sensors, variables, operators. | 4 |
| Elegant and ingenious solutions. |
RESULTS
In this section we will present and analyze the results obtained in two blocks: the first one will focus on the results of the CTt, while the second one will analyze the results obtained in the CTt (pre and post) and their relationship with those obtained in the Scratch project.
Comparative analysis of pre- and post-training CTt scores
Table 2 gives details of the reliability coefficients, which are considered acceptable for the ranges commonly accepted in the educational field.
| Scale | Cronbach's Alpha |
| Pre-test | 0.781 |
| Post-test | 0.835 |
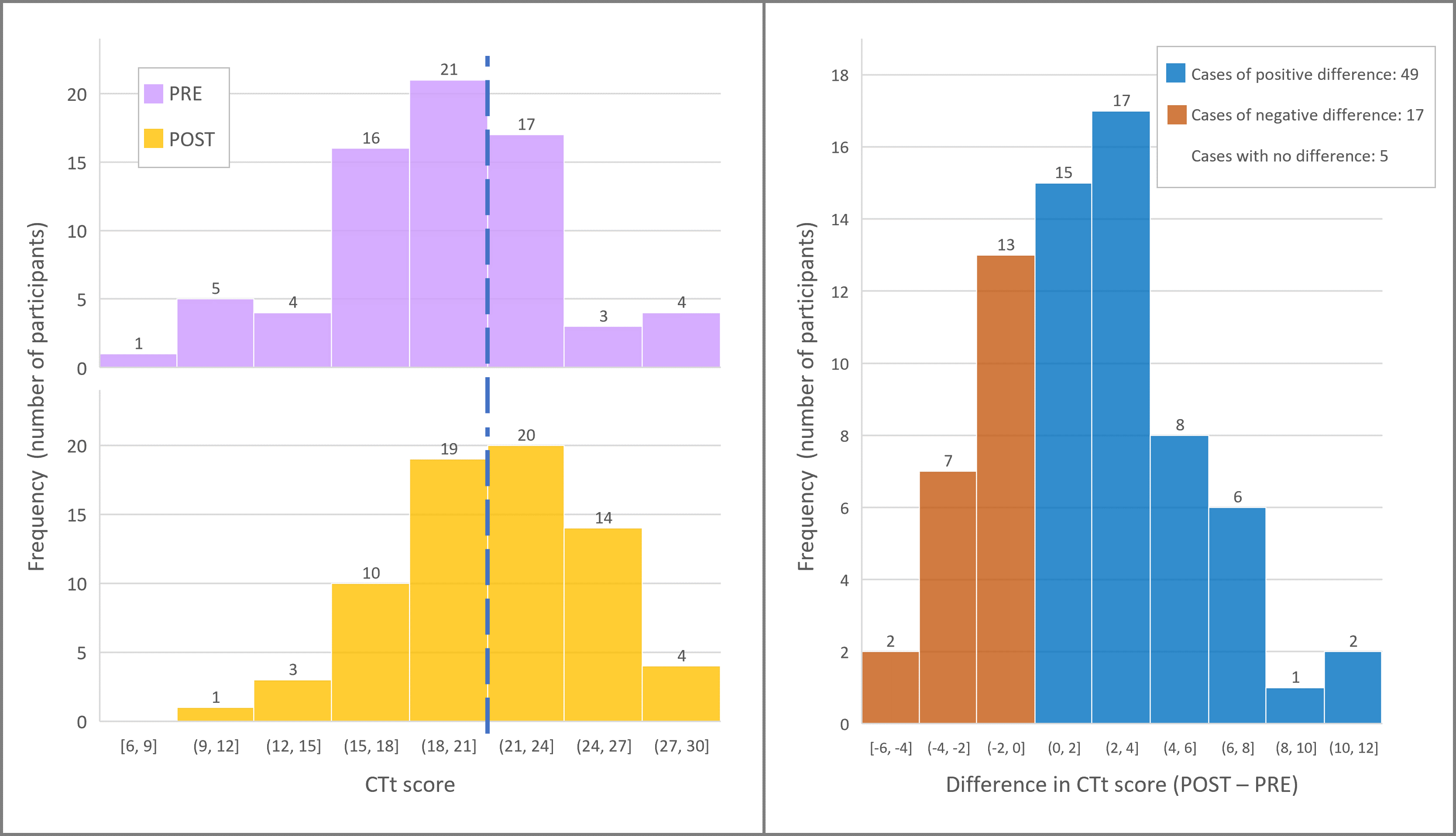
Figure 1a represents, on the same scale, the histograms or frequency plots of the participants' scores on the CT pre- and post-training tests. The Kolmogorov-Smirnov normality test for a sample confirms that both follow a normal or Gaussian distribution, which will allow us to use the means and standard errors as a valid description of the data and to use parametric statistics to perform comparison tests (Rubio Hurtado and Berlanga Silvente, 2012; Simpson, 2015). We can observe that in the distribution of the POST test there is a general displacement of the scores towards higher values than those of the PRE test, so that if we focus on score 21 (which lies between the intervals containing the PRE and POST mean, marked by the blue dashed line), we can see that before the training we have 47 values below or equal to it and 24 above it, and after the training these values become 33 and 38 respectively. Figure 1b shows the distribution of each participant's score difference between the POST and PRE tests. In addition to the fact that 49 of the differences are positive, 17 negative and in 5 cases there is no score difference, it is worth noting the asymmetry with respect to the 0 difference across the distribution, which denotes that the positive differences are significantly larger. An example of this is the fact that the maximum negative difference is 5 points while the maximum positive difference is 12 points. Thus, the graphs in Figure 1 show that between the PRE and POST tests there has been, on average, a development of CT according to the parameters measured by the CTt.
a) Frequency histogram of the scores obtained by the participants in the pre-training test (top) and in the post-training test (bottom) b) Frequency histogram of the difference in scores between the two tests obtained by each participant
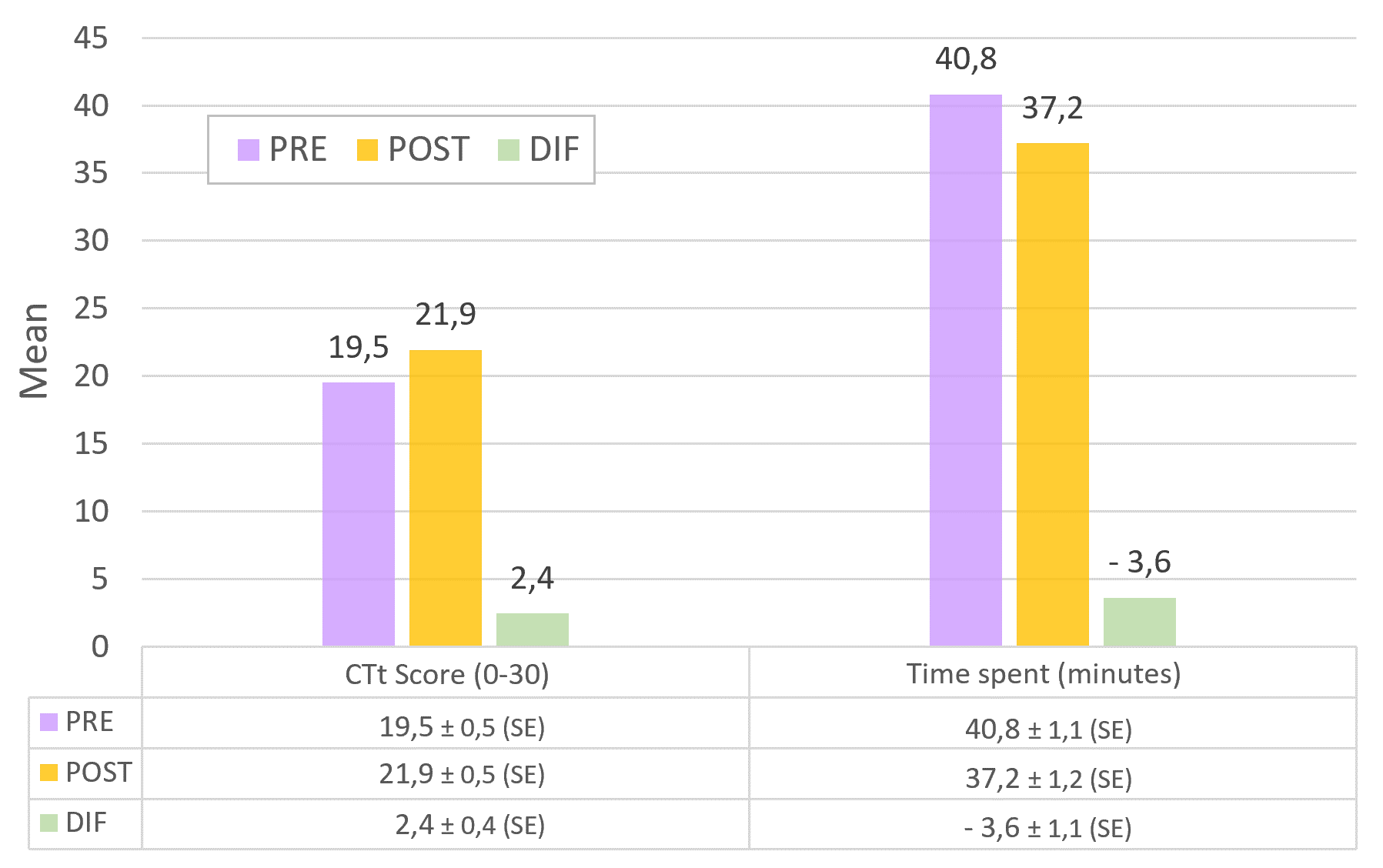
This development of the CT is shown quantified in Figure 2, where the means of the CTt score and the time students needed to complete it in the PRE and POST tests are indicated with their standard errors (SE) or standard error of the mean. As we can see, the mean CTt score has increased from 19.5 to 21.9 on a 30-point scale and there has been a decrease in the time taken to complete the test from 40.8 to 37.2 minutes. The differences in both cases are statistically significant with a p-value<0.001, i.e., we can state that the probability that the difference is not due to chance is greater than 99.9%. The practical significance measured by the sample size effect of Cohen's d is 0.6 in the case of differences in score and 0.4 in the case of differences in time.
Mean values of the CTt result and the time needed to solve it in the total population (71 participants between 2021 and 2022) applied pre-training (PRE) and post-training (POST) and their comparison (DIF). Their standard errors (SE) are also indicated
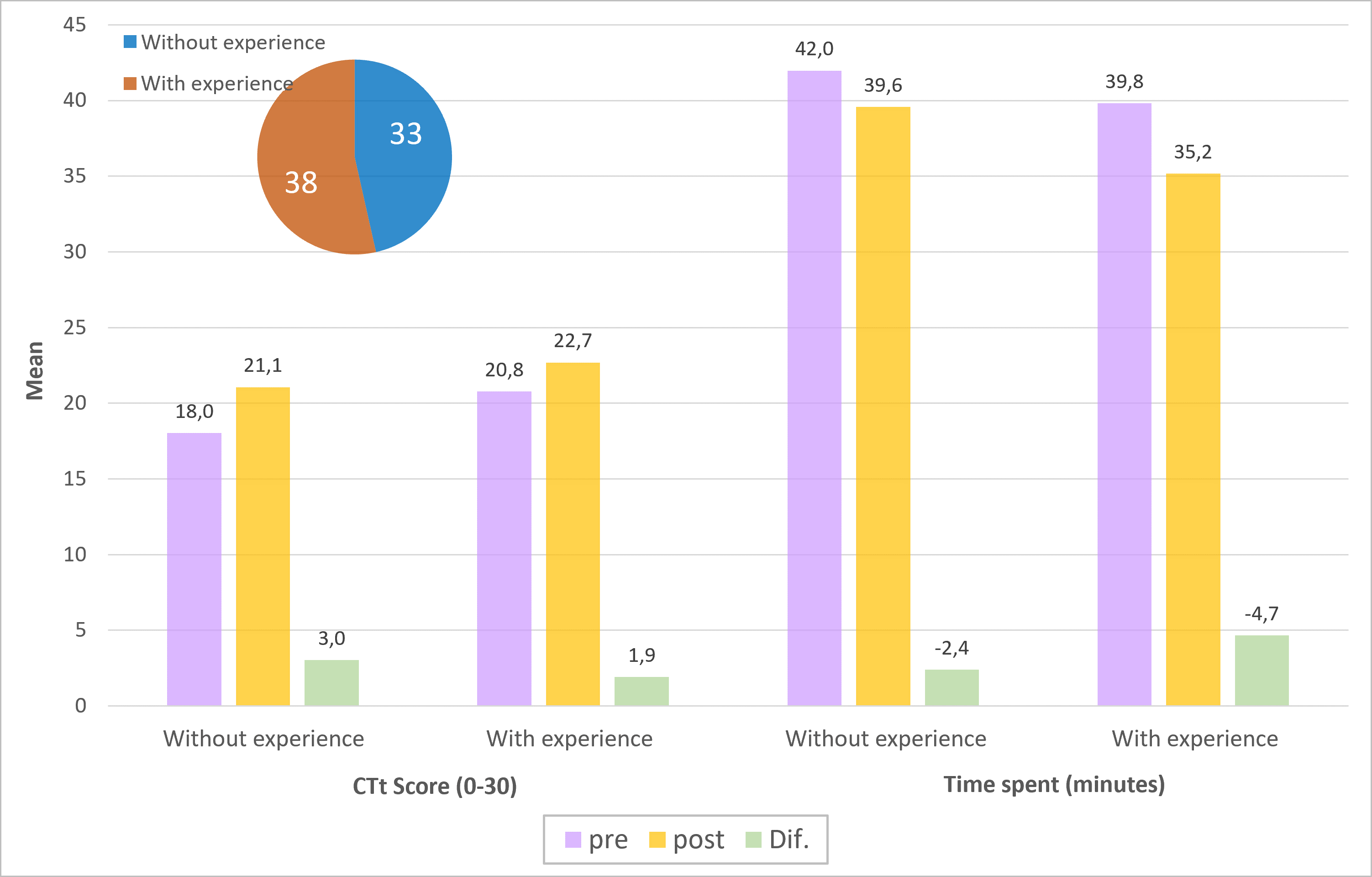
Next, we analyzed the data by grouping the participants according to whether they had previous experience in programming or robotics activities prior to entering university, at any stage of education in both formal and informal settings. Of the 71 participants, 33 reported no previous experience and 38 reported having some experience. Table 3 shows, for each of these two groups, the mean scores obtained in the CTt (PRE and POST) and the time taken to solve them. The differences obtained by comparing the results of the two CTt (PRE and POST) in the same group and by comparing the results of a single CTt (PRE or POST) between groups are also shown. To test the statistical significance of these differences we used, in the first case, the non-parametric test for paired samples Wilcoxon Signed Rank, and, in the second case, the non-parametric test for independent samples Mann-Whitney U. We considered the differences to be significant (not due to chance) for p-values<0.05.
| Average CTt score | Average time spent (minutes) | |||||
| PRE | POST |
DIF (POST-PRE) |
PRE | POST |
DIF (POST-PRE) |
|
| With experience (33 participants) | 18.0±0.8(SE) | 21.1±0.6(SE) | 3.1±0.6(SE) p<0.001, d=0.8 | 42.0±1.6(SE) | 39.6±1.8(SE) | -2.4±1.8(SE) p=0.1, d=0.2 |
| Without experience (38 participants) | 20.8±0.6(SE) | 22.7±0.7(SE) | 1.9±0.5(SE) p<0.001, d=0.6 | 39.8±1.5(SE) | 35.2±1.6(SE) | -4.6±1.5(SE) p=0.001, d=0.5 |
| Difference (with exp. - without exp.) | 2.8±1.0(SE) p=0.02, d=0.6 | 1.6±1.0(SE) p=0.08, d=0.4 | -2.2±2(SE) p=0.3, d=0.2 | -4.4±1.5(SE) p=0.04, d=0.4 | ||
If we focus on the mean score of the CTt, and compare between the two groups, we can see that prior to the training the students with previous experience obtain a score of 20.8 points and this is 2.8 points higher than the mean score of the students with no experience. This difference is significant, with p=0.02. After the training, the difference in the mean CTt score decreases and cannot be considered significant (p=0.08). When we compare the PRE and POST results of each group we can see ( Figure 3) that both groups have increased the mean score of the CTt, and this increase is more relevant in the group that had no previous experience. Therefore, insofar as there has been a development of the CTt in both groups, although unequal, the training has been able to partly compensate for the lack of previous experience.
It is worth noting that part of the ability in solving the CTt is also reflected in the time taken to solve it, and in the case of students with previous experience the decrease in time is relevant (4.6 minutes, p=0.001). Therefore, while for inexperienced students the increase in CT development is more evident in the CTt results (which increase more), students with previous experience show it in the time taken to complete it (which decreases more). This may indicate that, depending on the stage of CT development, the impossibility of passing certain test scores, which were already initially high, is reflected in the time spent.
Mean values of the CTt result and the time needed to solve it according to previous experience applied before the training (PRE) and after the training (POST) and their comparison (DIF)
To further analyze this aspect, we grouped the variables of the entire population into three samples, taking as a reference the score obtained in the pre-training CTt. Thus, from the terciles calculated in the distribution of the PRE score, we grouped the participants into the levels "lower pre-CT" (26 participants with an average score of 15.1), "middle pre-CT” (31 participants with an average score of 20.6) and "higher pre-CT" (14 participants with an average score of 25.4) and calculated for each of them the results obtained in the post-training CTt. In Figure 4 we can see, for each group, the mean scores, the differences in mean score between the POST and PRE test and the differences in mean time taken to perform the test.
Mean values of the CTt result and the time needed to solve it (PRE and POST) grouping the population according to initial result
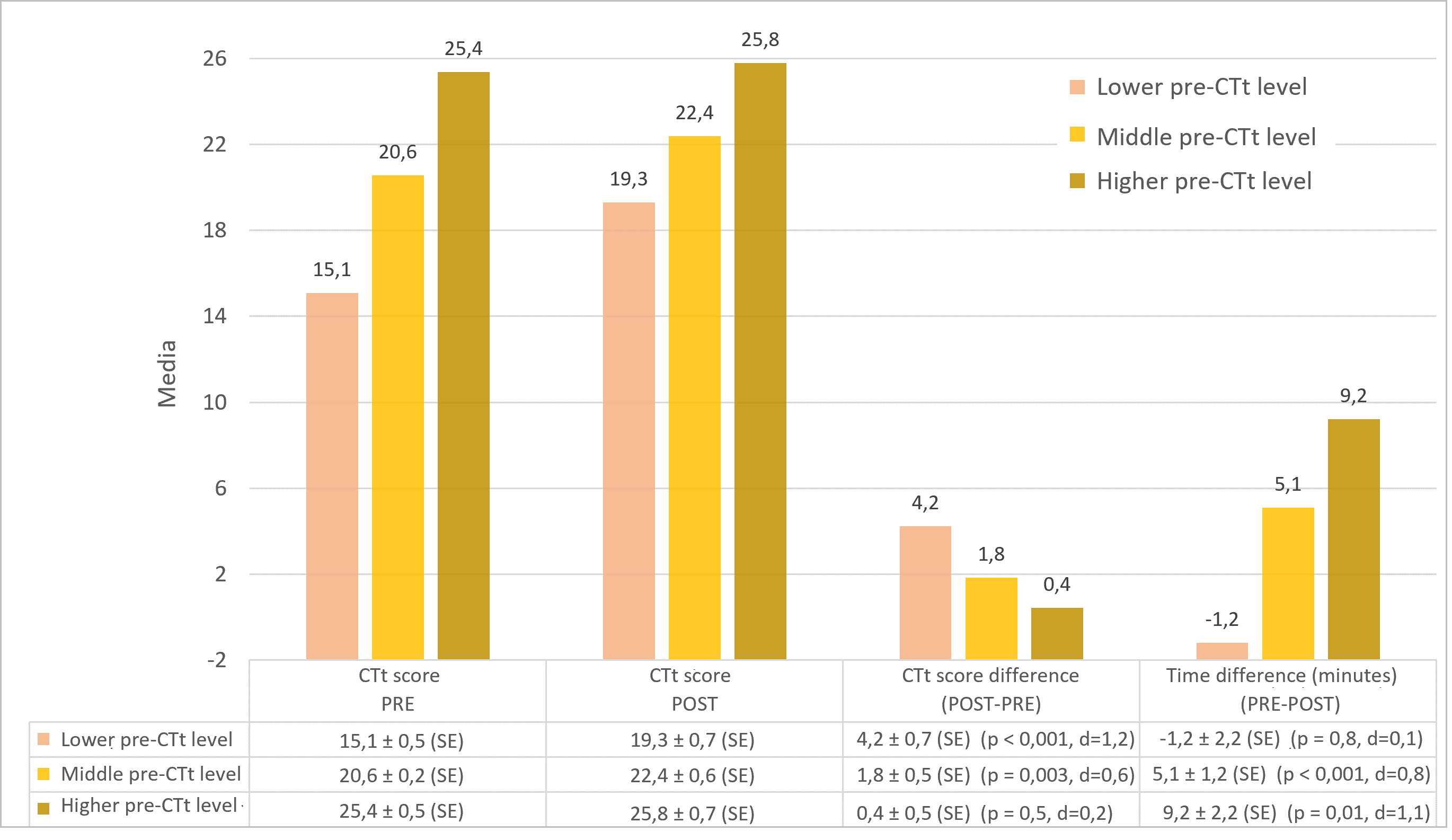
We observe that, in the lower level group, there has been a significant increase in the CTt score (4.2 points; p=0.001); in the medium level group there has also been a significant increase, although it has been lower (1.8 points; p=0.003); and in the higher level group the increase in the CTt score is not significant. However, if we focus on the average time needed to solve the test, the effect is different: in the lower level it has remained without significant changes and in the medium and higher levels it has decreased significantly, so that the group with medium level has needed an average of 5.1 minutes less than in the PRE test to solve the POST test and the group with higher level has done it in an average time of 9.2 minutes less. Therefore, the results show that the training has helped the three groups in the development of CT and has had a certain equalizing effect (the group with the lowest initial score has shown a greater increase), and has improved the agility in its use in those students who already started from a high level, who have needed less time to do it. In the analysis of the correlation between the PRE and POST CTt scores of the whole sample, a positive, moderately high and statistically significant correlation was obtained, with a value of r=0.67. This can be interpreted in terms of test reliability and stability. The fact that total convergence is not reached can be explained by the difference in the increase in learning according to the starting level found in the analysis of the samples by levels.
Relationship between programming with Scratch and the results of the CTt
We would now like to analyze whether there is a relationship between the results of Scratch Programming according to the categories shown in Table 1 and the results of the CTt, focusing on two main areas of interest: firstly, how the starting point of the CTt influences the results of Scratch Programming; secondly, how the level of development of Scratch Programming is reflected in the final CTt.
As a frame of reference, regarding the total score in Scratch Programming according to the categories in Table 1 obtained by the 71 participants, the minimum score is 4 points and the maximum is 12, the mean value is 9.3±0.2 (SE) points, the median is 10 points, and the mode is 11. The evaluation was carried out by a single researcher expert in Scratch programming, in a double cycle (weighting and review), in order to guarantee the homogeneity of the criteria applied.
In order to analyze whether the starting point indicated by the pre-training CTt can be related to the outcome of the Scratch project, we calculated the mean values of the score by grouping the population according to the 3 samples "Lower pre-CTt level", "Middle pre-Ctt level" and "Higher pre-CTt level" that had been used in the comparison between the PRE and POST CTt, and we obtained the results shown in Table 4. As we can see, there is no significant variation in the results related to CT in the Scratch project between the participants who started at the medium level and those who started at the lower level. There is, however, a certain difference with respect to the other levels in the results obtained by those participants who started from a higher level, who also obtained better results in programming. This result may support, on the one hand, the compensatory aspect of the training with respect to the CT level according to the parameters of the CTt, especially between the lower and middle pre-CT level groups; and, on the other hand, the fact that the programming elements identified as characteristic of the parameters measured by the CTt are applied to their Scratch projects by the students who started from a higher level.
| PRE-CTt level | Lower pre-CTt | Middle pre-CTt | Higher pre-CTt |
| CT Scoring in Scratch Programming | 8.8±0.4(SE) | 9.1±0.4(SE) | 10.9±0.2(SE) |
| Differences | Lower-Middle: 0.3±0.5(SE) p=0.8 | Higher-Middle: 1.8±0.6 (SE) p=0.02 | Higher-Lower: 2.1±0.6(SE) p=0.006 |
At this point, we can ask ourselves whether having created a complex program (using a computer language, using ingenuity and optimization that works) is related to the results of the CTt. To analyze this relationship between the results of Scratch programming and the results of the CTt after the creation of the project, we have grouped the participants according to the levels of lower programming, medium programming, and higher programming, taking as a reference the terciles of the programming score distribution. Thus, in the Lower programming level group (score range 4 to 8 points) there are 20 participants; in the Middle programming level (score range 9 and 10 points) there are 25 participants; and in the Higher programming level (score range 11 and 12 points) there are 26 participants. Table 5 shows the average total programming score for each of these groups and their scores on the CTt. Differences in CTt scores between the three levels are also shown with their statistical significance.
| Programming level |
Lower [4,8] 20 participants |
Middle [9,10] 25 participants |
Higher [11,12] 26 participants |
| Total programming | 6.6±0.3(SE) | 9.6±0.1(SE) | 11.27±0.09(SE) |
| POST CTt Score | 18.9±0.8(SE) | 21.6±0.7(SE) | 24.6±0.6(SE) |
| Differences | Lower-Middle: 2.7±1.0(SE) p=0.03 | Higher-Middle: 3.1±0.9(SE) p=0.007 | Higher-Lower: 5.7±1.0 (SE) p<0.001 |
We can observe that there is a gradation in the CTt score that also corresponds to the gradation of the three programming levels, so that the students belonging to the Lower programming level group obtain an average score in the POST CTt of 18.9 and this is surpassed by 2.7 points by the students of the Middle programming level and by 5.7 points by the students of the Higher programming level. In order to check the statistical significance of the differences between the groups, the non-parametric Kruskal-Wallis test was used to compare more than 2 groups and it was considered that these differences were not due to chance for p<0.05. As can also be seen in Table 5, the differences in the POST CTt results are significant in the pairwise comparisons of the 3 groups. Figure 5 shows the POST CTt score gradation according to the programming level groups.
Distribution of the results of the CTt (post) according to the results of the Scratch project
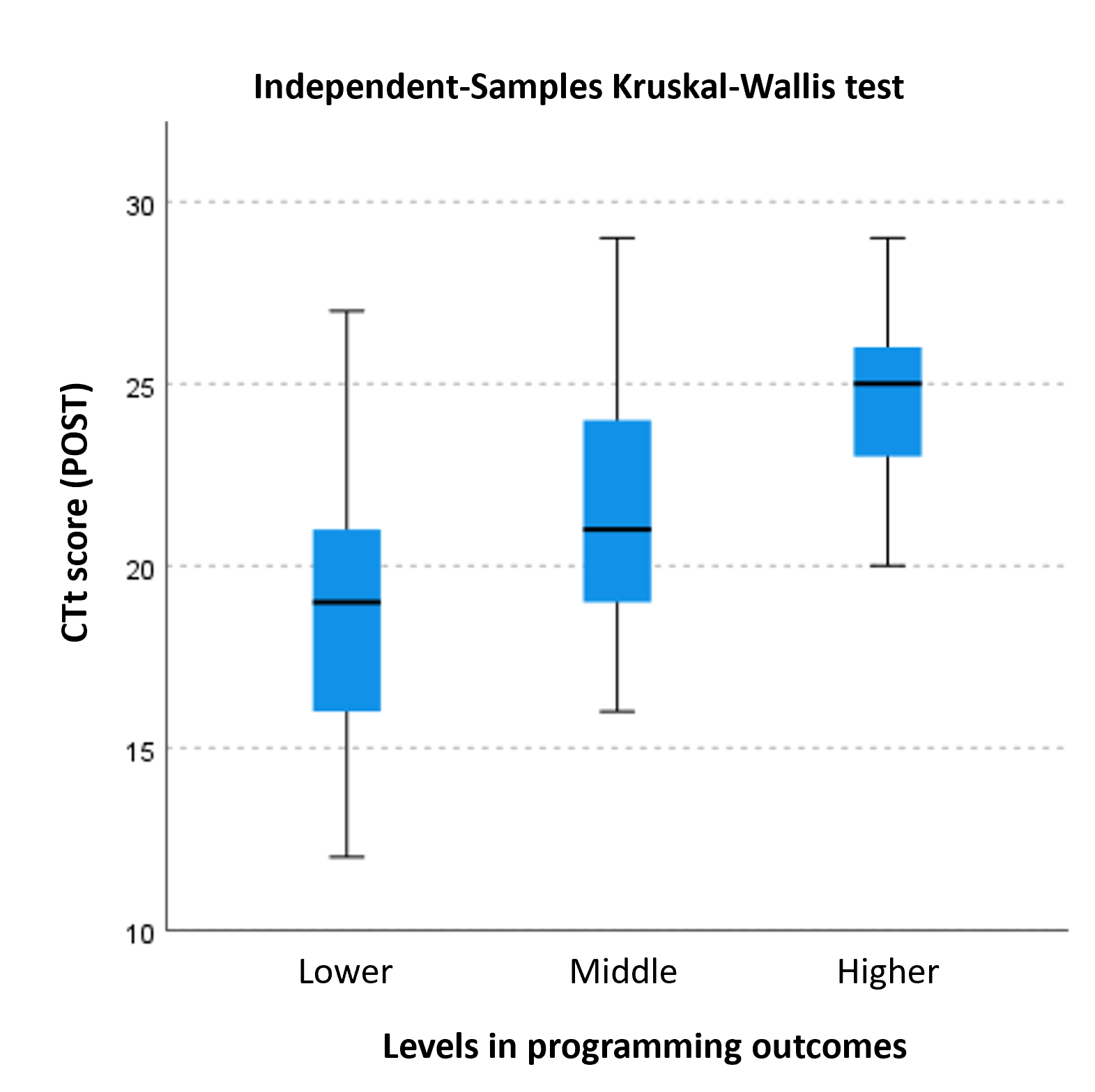
The result reflects that work in Scratch that involves care and dedication can help in the development of the CT regardless of the level of CT development from which it was started. Therefore, getting a good result programming Scratch does not depend so much on the initial CT level (as its creators say, Scratch has a low floor from which you can evolve to a ceiling as high as you want (Resnick, 2018)); on the contrary, having done a planned and conscious (not incidental) work in Scratch exploring and using its different possibilities and dimensions has an impact on the development of the subsequent CT level.
To complete the analysis of the relationship between the results of Scratch Programming and the results of the CTt, we present the results of the correlations between the two tests, as they can be interpreted in terms of predictive validity of the CTt (in the case of the correlation "CTt-pre * Scratch projects" and in terms of concurrent/convergent validity of the test, in the case of the correlation "CTt-post * Scratch projects" in an approach similar to Román-González et al. (2019). The value of the correlation "CTt * Scratch projects" is r=0.40 and is statistically significant. The convergence is partial, and agrees with the results obtained in the analysis by terciles according to starting level in the CTt score, which indicate that the participants who started from the lowest and middle levels have obtained similar results in programming, significantly surpassed by the participants from the highest level (Table 4), so that the Scratch training has had the compensatory effect that is observed throughout the analysis. The value of the correlation "CTt * Scratch projects" is r=0.59. This value, which is higher than in the case of the PRE CTt agrees with the results of the analysis by terciles according to the results of the programming (Table 5), which confirms that the concepts and skills acquired during the Scratch training and the effort in carrying out the project do not depend so much on the initial CT level, but do imply a development in this as is reflected in the final CT level according to the CTt.
DISCUSSION AND CONCLUSIONS
Based on everything we have been referring to in the results section, it is now time to try to synthesize the main findings and interpret them in the light of what we already know from previous literature. For the sake of clarity of discourse, we will try to organize this reflection into two main parts: the first part focuses on the validation of the training itself (to what extent an intensive training experience such as the one we present allows CT to be developed, in the style of what we saw in Pala and Türker (2021), for example). Secondly, we will focus on the relationship between this CT development and the creation of a Scratch project.
In relation to the first block, we note the following three important ideas. (1) There is a generalized development of CT according to the parameters measured by the CTt, which shows that the training proposal allows all students to achieve their learning objectives. (2) The participants with no previous experience start from a lower CT level than the experienced participants, in effect; but the former experience a higher average increase in the CTt score than the latter. However, in the more experienced group, after the training, the time needed to take the test decreases. And (3) the analysis of the population analyzed in three initial levels according to the PRE-CTt score and the analysis of the POST-CTt results for each of these groups shows that students starting from lower levels experience a higher average increase in the CTt score than students starting from higher levels. In the higher levels the development of CT is shown in the decrease of the time needed in the resolution.
From these three points we conclude that the training fulfils the objective of developing CT according to the parameters measured by the CTt, as already documented, with a single cohort, in Peracaula-Bosch and González-Martínez (2022); but not only that, it also has an equalizing effect on the ability to solve the problems posed by the test and speeds up their resolution in those students who already started from such a high level that it was difficult to improve their scores. To an extent, this is in line with what Wong (2023) points out with the school population: "The results of the study show that children, regardless of their prior problem-solving skills, significantly improve their understanding of basic CT through programming, particularly for low-performing students" (p. 17). In its simplicity and economy, the training strategy is therefore effective in general, and especially for those with less advantageous starting points (Morze et al., 2022). And it is especially important if we bear in mind the need to guarantee a sufficient set of technical user skills to tackle the second part of the course, which is dedicated to CT didactics (and therefore it is proposed for this second part that students not only develop their own CT, but also know enough about Scratch to be able to transfer it to their didactic planning), in line with what Rich, Larsen and Mason (2021) and Collado-Sánchez et al. (2021) point out.
In relation to the second block, dedicated to analyzing the relationship between the level of programming and the results of the CTt, we have broken down the study into two steps. We found that, on the one hand, the results of the CTt prior to training are related to the competences and skills demonstrated by the students in the development of a complex programming project with Scratch in the case of subjects who started with a high score in the CTt. For the students who scored at the lower and intermediate levels, this relationship is not significant, so that the learning outcomes are more important. On the other hand, the score in competences and skills shown in the use of programming elements and concepts in the Scratch project does show a significant relationship with the results of the POST CTt, which indicates that the training carried out through this resource and with the design used has had an impact on the development of the CTt ( Pala & Türker, 2021; Rich, Mason & O'Leary, 2021), despite the short time available for this, which requires an intensive approach (Ung et al. 2022).
Finally, despite these good results (both for the confirmation of previous experiences and for the deepening of the specific analysis of the Scratch project), we must recognize limitations in the research that, at the same time, become possible future lines of investigation. The final evaluation of the students' work also took into account other factors such as creativity, the use of artistic elements, and the quality of the writing of the final document in which they explained the process, the learning obtained and the transfer and its didactic use at school. However, for our study we limit ourselves to the analysis of the elements that are directly related to the development of CT according to the parameters measured by the CTt. There is no doubt that the complexity of CT itself (Wing, 2014) should lead us to consider further analyses. As Acevedo-Borrega et al. (2022) and Morze et al. (2022) point out, we must go deeper into the conceptualization of CT in the field of education, on a two-way path between research and practice.
REFERENCES
Acevedo-Borrega, J. (2016). El pensamiento computacional en la educación obligatoria. Una revisión sistemática de la literatura [Tesis de Maestría, Universidad de Extremadura]. DEHESA. Repositorio institucional Universidad de Extremadura. http://hdl.handle.net/10662/5356
Acevedo-Borrega, J., Valverde-Berrocoso, J., & Garrido-Arroyo, M. D. C. (2022). Computational Thinking and Educational Technology: A Scoping Review of the Literature. In Education Sciences, 12(1), Artículo 39. https://doi.org/10.3390/educsci12010039
Angeli, C., Voogt, J., Fluck, A., Webb, M., Cox, M., Malyn-Smith, J., & Zagami, J. (2016). A K-6 Computational Thinking Curriculum Framework: Implications for Teacher Knowledge. Educational Technology & Society, 19(3), 47-57. https://www.jstor.org/stable/jeductechsoci.19.3.47
Bocconi, S., Chioccariello, A., Dettori, G., Ferrari, A., & Engelhardt, K. (2016a). Developing Computational Thinking in Compulsory Education. Implications for policy and practice. https://doi.org/10.2791/792158
Bocconi, S., Chioccariello, A., Dettori, G., Ferrari, A., Engelhardt, K., Kampylis, P., & Punie, Y. (2016b). Developing Computational Thinking: Approaches and Orientations in K-12 Education. In Proceedings of the EdMedia 2016 Conference (pp. 13-18). Association for the Advancement of Computing in Education (AACE). http://www.learntechlib.org/p/172925/
Bustillo, J., & Garaizar, P. (2015). Scratching the surface of digital literacy... but we need to go deeper. Proceedings of the Frontiers in Education Conference (FIE), 1-4. https://doi.org/10.1109/FIE.2014.7044224
Butler, D., & Leahy, M. (2021). Developing preservice teachers’ understanding of computational thinking: A constructionist approach. British Journal of Educational Technology, 52(3), 1060-1077. https://doi.org/10.1111/bjet.13090
Collado-Sánchez, M., García-Peñalvo, F. J., & Pinto-Llorente, A. M. (2021). Computational thinking competences training for primary education teachers. In Ninth International Conference on Technological Ecosystems for Enhancing Multiculturality (TEEM'21), 758-762. https://doi.org/10.1145/3486011.3486544
Dobgenski, J., & Garcia Silva, A da F. (2022). A practical experience in pre-service teacher education focusing on computational thinking. 12th Congress of the European Society for Research in Mathematics Education (CERME12), Feb 2022, Bozen-Bolzano, Italia. https://hal.archives-ouvertes.fr/hal-03748506
Estebanell, M., López, V., Peracaula-Bosch, M., Simarro, C., Cornellà, P., Couso, D., González-Martínez, J., Alsina, À., Badillo, E., & Heras, R. (2018). Teacher training in Computational Thinking. Teaching Guide. https://pecofim.wixsite.com/pecofim/guia-didactica
European Commission / EACEA / Eurydice. (2012). Developing Key Competences at School in Europe: Challenges and Opportunities for Policy. Eurydice Report. Luxembourg: Publications Office of the European Union. https://doi.org/10.2797/93204
Fluck, A., Webb, M., Cox, M., Angeli, C., Malyn-smith, J., Voogt, J., & Zagami, J. (2016). Arguing for Computer Science in the School Curriculum. Educational Technology & Society, 19(3), 38-46. https://www.jstor.org/stable/jeductechsoci.19.3.38
Furber, S. (2012). Shut down or restart? The way forward for computing in UK schools. The Royal Society. https://royalsociety.org/-/media/education/computing-in-schools/2012-01-12-computing-in-schools.pdf
González-Martínez, J., Estebanell, M., & Peracaula-Bosch, M. (2018). ¿Robots o programación? El concepto de Pensamiento Computacional y los futuros maestros. Education in the Knowledge Society (EKS), 19(2), 29-45. https://doi.org/10.14201/eks20181922945
Grover, S., & Pea, R. (2013). Computational Thinking in K–12: A Review of the State of the Field. Educational Researcher, 42(1), 38-43. https://doi.org/10.3102/0013189X12463051
Kong, S. C., Lai, M., & Li, Y. (2023). Scaling up a teacher development program for sustainable computational thinking education: TPACK surveys, concept tests and primary school visits. Computers & Education, 194, Artículo 104707. https://doi.org/10.1016/j.compedu.2022.104707
Lamprou, A., & Repenning, A. (2018). Teaching How to Teach Computational Thinking. In Proceedings of 23rd Annual ACM Conference on Innovation and Technology in Computer Science Education (ITiCSE’18). ACM. https://doi.org/10.1145/3197091.3197120
Li, Q. (2021). Computational thinking and teacher education: An expert interview study. Human Behavior and Emerging Technologies, 3, 324-338. https://doi.org/10.1002/hbe2.224
Mason, S. L., & Rich, P. J. (2019). Preparing Elementary School Teachers to Teach Computing, Coding, and Computational Thinking. Contemporary Issues in Technology and Teacher Education, 19(4), 790-824. Waynesville, NC USA: Society for Information Technology & Teacher Education https://citejournal.org/volume-19/issue-4-19/general/preparing-elementary-school-teachers-to-teach-computing-coding-and-computational-thinking
Mishra, P., & Koehler, M. J. (2006). Technological Pedagogical Content Knowledge: A Framework for Teacher Knowledge. Teachers College Record, 108(6), 1017-1054. https://doi.org/10.1111/j.1467-9620.2006.00684.x
Moreno León, J., Román-González, M., Robles, G. (2022). Escuela de Pensamiento Computacional e Inteligencia Artificial 20/21: Enfoques y propuestas para su aplicación en el aula. Resultados de la investigación. Publicaciones Ministerio de Educación y Formación Profesional. https://sede.educacion.gob.es/publiventa/d/25861/19/0
Morreale, P., Jimenez, L., Goski, C., & Stewart-Gardiner, C. (2012). Measuring the impact of computational thinking workshops on high school teachers. Journal of Computing Sciences in Colleges, 27(6), 151-157. https://dl.acm.org/doi/abs/10.5555/2184451.2184486
Morze, N., Barna, O., & Boiko, M. (2022). The relevance of training primary school teachers computational thinking. In Proceedings of the 17th International Conference on ICT in Education Research and Industrial Applications: Integration, Harmonization and Knowledge Transfer (ICTERI 2021), 3104, 141-153. https://ceur-ws.org/Vol-3104/paper218.pdf
Pala, F. K., & Türker, P. M. (2021). The effects of different programming trainings on the computational thinking skills. Interactive Learning Environments, 29(7), 1090-1100. https://doi.org/10.1080/10494820.2019.1635495
Papert, S. (1980). Mindstorms. Children, computers and powerful ideas. Basic Books.
Peracaula-Bosch, M., Estebanell-Minguell, M., Couso, D., & González-Martínez, J. (2020). What do pre-service teachers know about computational thinking? Aloma. Revista de Psicologia, Ciències de l’Educació i de l’Esport, 38(1), 75-86. https://doi.org/10.51698/aloma.2020.38.1.75-86
Peracaula-Bosch, M., & González-Martínez, J. (2022). Developing computational thinking among pre-service teachers. QWERTY. Open and Interdisciplinary Journal of Technology, Culture and Education, 17(1), 28–44. https://doi.org/10.30557/QW000049
Pérez-Marín, D., Hijón-Neira, R., Bacelo, A., & Pizarro, C. (2020). Can computational thinking be improved by using a methodology based on metaphors and scratch to teach computer programming to children? Computers in Human Behavior, 105(August 2018), Artículo 105849. https://doi.org/10.1016/j.chb.2018.12.027
Resnick, M. (2018). Lifelong Kindergarten. Cultivating Creativity through Projects, Pasion, Peers and Play. The MIT Press. https://doi.org/10.7551/mitpress/11017.001.0001
Rich, P. J., Larsen, R. A., & Mason, S. L. (2021). Measuring teacher beliefs about coding and computational thinking. Journal of Research on Technology in Education, 53(3), 296-316. https://doi.org/10.1080/15391523.2020.1771232
Rich, P. J., Mason, S. L., & O’Leary, J. (2021). Measuring the effect of continuous professional development on elementary teachers’ self-efficacy to teach coding and computational thinking. Computers & Education, 168, Artículo 104196. https://doi.org/10.1016/j.compedu.2021.104196
Román-González, M. (2016). Codigoalfabetización y Pensamiento Computacional en Educación Primaria y Secundaria: validación de un instrumento y evaluación de programas [Tesis Doctoral, Universidad Nacional de Educación a Distancia]. Repositorio Institucional de la Universidad Nacional de Educación a Distancia. https://doi.org/10.1007/978-981-13-6528-7_6
Román-González, M., Moreno-León, J., & Robles, G. (2019). Combining assessment tools for a comprehensive evaluation of computational thinking interventions. In S. Kong & H. Abelson (Eds.), Computational thinking education (pp. 79-98). Springer. https://doi.org/10.1016/j.chb.2016.08.047
Román-González, M., Pérez González, J. C., & Jiménez Fernández, C. (2017). Which cognitive abilities underlie computational thinking? Criterion validity of the Computational Thinking Test. Computers in Human Behavior 72(July), 678-691. https://doi.org/10.1016/j.ijcci.2018.06.004
Román-González, M., Pérez-González, J. C., Moreno-León, J., & Robles, G. (2018). Can computational talent be detected? Predictive validity of the Computational Thinking Test. International Journal of Child-Computer Interaction, 18(November), 47-58. https://doi.org/10.1016/j.ijcci.2018.06.004
Rubio Hurtado, M. J., & Berlanga Silvente, V. (2012). Cómo aplicar las pruebas paramétricas bivariadas t de Student y ANOVA en SPSS. Caso práctico. REIRE Revista d’Innovació i Recerca en Educació, 5(2), 83-100. https://doi.org/10.1344/reire2012.5.2527
Simpson, S. H. (2015). Creating a Data Analysis Plan: What to Consider When Choosing Statistics for a Study. The Canadian Journal of Hospital Pharmacy, 68(4), 311-317. https://doi.org/10.4212/cjhp.v68i4.1471
Ung, L. L., Labadin, J., & Mohamad, F. S. (2022). Computational thinking for teachers: Development of a localised E-learning system. Computers & Education, 177(February). Artículo 104379. https://doi.org/10.1016/j.compedu.2021.104379
Wing, J. (2006). Computational Thinking. Communications of the ACM, 49(3), 33-35. https://doi.org/10.1145/1118178.1118215
Wing, J. (10 de enero 2014). Computational Thinking benefits society. Social Issues in Computing. http://socialissues.cs.toronto.edu/index.html%3Fp=279.html
Wong, G. K. W. (2023). Amplifying children’s computational problem-solving skills: A hybrid-based design for programming education. Education and Information Technologies. https://doi.org/10.1007/s10639-023-11880-9
Date of reception: 01 June 2023
Date of acceptance: 30 August 2023
Date of publication in OnlineFirst: 19 October 2023
Date of publication: 01 January 2024
